程序设计：算法和数据结构 笔记1

基础篇

基础概念

复杂性评估

• 时间复杂度：评估执行程序所需要的时间。可以估算出程序对计算机处理器的使用程序
• 空间复杂度：评估执行程序 所需的存储空间。可以估算出程序 对计算机内存的使用程度

“复杂度”大多数情况下是指的时间复杂度

大O表示法：大O表示法是一种评估算法效率的“标尺”，以诸如$O(n)$、$O(n^2)$的形式表示算法的效率，其中n为问题的数据大小。

常用的复杂度比较

$ n $	$ log(n) $	$ \sqrt n$	$ nlog(n) $	$$n^2 $$	$ 2^n $	$ n! $
5	2	2	10	25	32	120
10	3	3	30	100	1024	3628800
20	4	4	80	400	1048576	约$ 2.4 \times 10^{18}$
50	5	7	250	2500	约$ 10^{15}$	约$ 3 \times 10^{64}$
100	6	10	600	10000	约$ 10^{30}$	约$ 9.3\times 10^{157}$
1000	9	31	9000	$ 10^6$	约$ 10^{300}$	约$ 4 \times 10^{2567}$
$10^4$	13	100	$ 1.3\times 10^{5}$	$ 10^9$	约$ 10^{3000}$	约$ 10^{35660}$
$10^5$	16	316	$ 1.6 \times 10^{6}$	$ 10^{10}$	约$ 10^{30000}$	约$ 10^{456574}$
$ 10^6$	19	100	$ 1.9 \times 10^{7}$	$ 10^{12}$	约$ 10^{300000}$	约$ 10^{5565709}$

稳定排序

是指在出现多次相同数据时，能保证稳定输出的排序算法

初等排序

排序	最好	最坏	稳定情况
插入排序	N（有序）	$O(N^2)$	稳定
冒泡排序	$O(N)$	$O(N^2)$	稳定
选择排序	$O(N^2)$	$O(N^2)$	不稳定
希尔排序	$O(N)$	$O(N^2)$	不稳定

插入排序

** 步骤：**

1. 从第一个元素开始，该元素可以认为已经被排序
2. 取出下一个元素，在已经排序的元素序列中从后向前扫描
3. 如果该元素（已排序）大于新元素，将该元素移到下一位置
4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
5. 将新元素插入到该位置中
6. 重复步骤2

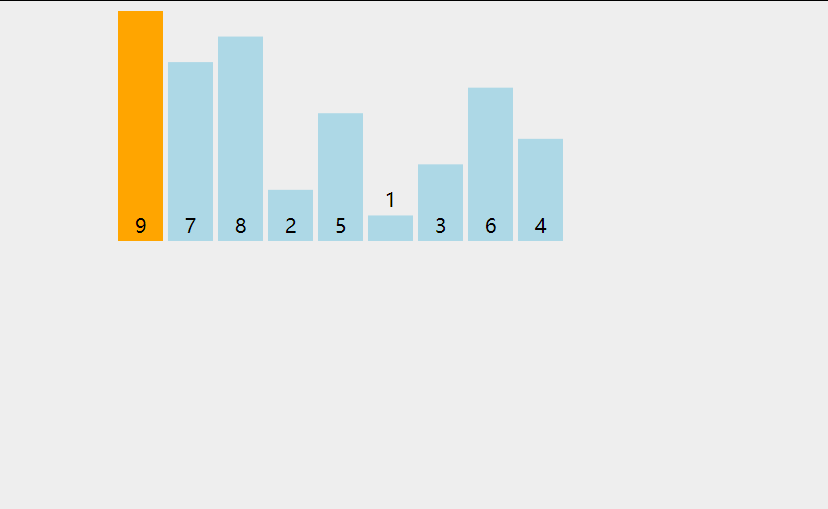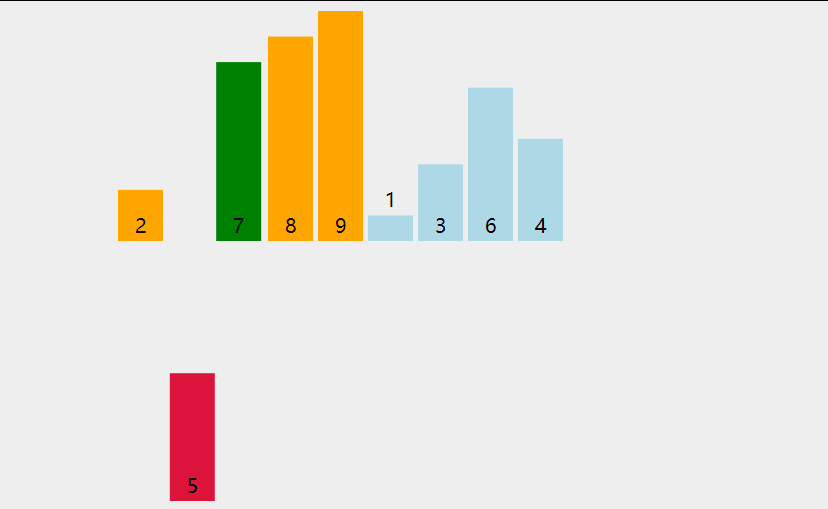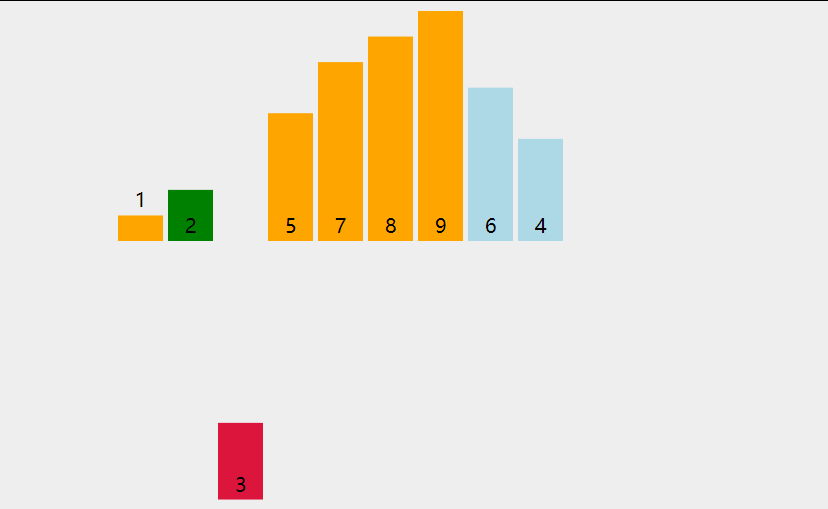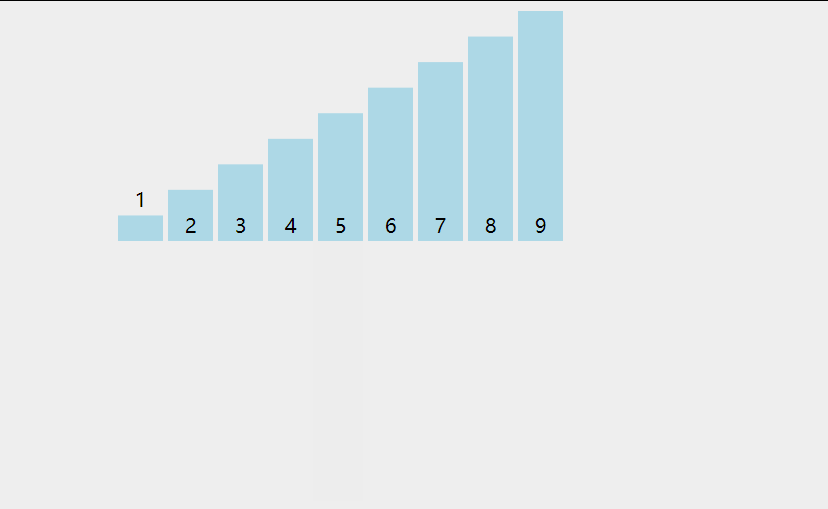
void InsertSort(int a[],int n)
{
    for(int i=0;i<n;i++)
    {
        int j=i-1;
        if(a[i]<a[i-1]){ //若第i个元素小于第i-1个元素,移动有序序列插入------大于的话则直接插入 
        int swap=a[i];  //存储将要排序的元素 
        a[i]=a[i-1];   //向后移动一个元素 
        while(swap<a[j])//查询将要插入的位置 
        {
            a[j+1]=a[j];
            j--;       //元素后移 
        }
        a[j+1]=swap;//循环结束 插入到指定位置 
    }    
    }
}

冒泡排序

** 步骤：**

1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
3. 针对所有的元素重复以上的步骤，除了最后一个。
4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

#include<stdio.h>
void BuddleSort(int a[],int n){
     
    for(int i=0;i<n-1;i++){
        for( int j=0;j<n-i-1;j++){
            if(a[j]>a[j+1]){
                int swap=a[j];
                a[j]=a[j+1];
                a[j+1]=swap;
            }
        }
    }
} 

选择排序

步骤：

1. 未排序序列中找到最小元素，存放到排序序列的起始位置。
2. 再从剩余未排序元素中继续寻找最小元素，然后放到排序序列末尾。
3. 以此类推，直到所有元素均排序完毕。

void SelectSort(int a[],int n)
{
    for(int i=0;i<n-1;i++)
    {
        int min=i;  //存放数组最小值的位置 
        
        for(int j=i+1;j<n;j++)
        {
            if(a[j]<a[min]){
                min=j;   //找出最小值，并记录位置 
            }
         } 
         if(min!=i) //最小元素与第i个元素互换位置 
         {
            int swap=a[min];
             a[min]=a[i];
             a[i]=swap;
         }
    }
}

希尔排序

步骤：

1. 选取间隔为g的元素进行插入排序
2. 缩小g的范围，新的g与原g互质
3. 重复执行步骤1，2
4. 最后选取g=1执行一次插入排序

insertionSort(A,n,g){
    for i = g to n-1
        v=A[i]
        j=i-g
        while j>=0 && A[j]>v
            A[j+g]=a[j]
            j=j-g
            cnt++
         A[j+g]=v
}
shellSort(A,n){
    cnt=0;
    m=?;
    g[]={……,1};
    for i=0 to m-1
        insertionSort(A,n,g[i])
}

注： 最后一定要执行一次g=1的普通 插入排序 ，确保正确

参考教材：《挑战程序设计竞赛2 算法数据结构》

参考资料：https://www.cnblogs.com/xaimicom/p/9189471.html