介绍

根据公式，将原有的8个问题换成七个问题，使得时间复杂度降低

两个矩阵A B相乘时，将A, B, C分成相等大小的方块矩阵
C的话为
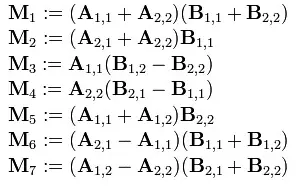
改进后的公式时间复杂度能够降低到 $O(n^{log_27})=O(n^{2.807})$

代码

#include <iostream>
#include <vector>
#include <math.h>
using  namespace std;
typedef vector<vector<int>> Matrix; //简写，方便，用到的地方多
/**
 * 根据公式，有加减乘三个方法，分别实现
 */
void display(Matrix arr){
    int r= arr.size(); //行数
    int c=arr[0].size();//列数
    for (int i = 0; i < r; ++i) {
        for (int j = 0; j < c; ++j) {
            cout<<arr[i][j]<<"\t";
        }
        cout<<endl;
    }
}
// 矩阵相减
Matrix MatrixSub(Matrix a,Matrix b){
    int row= a.size(); //行数
    int col=a[0].size();//列数
    // 相减，然后放到新的矩阵中
    Matrix c(row);
    for (int i = 0; i < row; ++i) {
        vector<int> t;
        for (int j = 0; j < col; ++j) {
            t.push_back(a[i][j]-b[i][j]);
        }
        c[i].insert(c[i].begin(),t.begin(),t.end());
    }
    return c;

}
//矩阵相加
Matrix MatrixAdd(Matrix a,Matrix b){
    int row= a.size(); //行数
    int col=a[0].size();//列数
    Matrix c;
    // 相减，然后放到新的矩阵中
    for (int i = 0; i < row; ++i) {
        vector<int> t;
        for (int j = 0; j < col; ++j) {
            t.push_back(a[i][j]+b[i][j]);
        }
        c.push_back(t);
    }
    return c;
}
// 拆分矩阵，拆成四个，放在vector中返回
// 下标为0 的是 左上  1的右上
// 下标为2 的是 左下  3的右下
vector<Matrix> split(Matrix a){
    vector<Matrix> t;
    int row= a.size(); //行数
    int col=a[0].size();//列数
    Matrix v1(row/2);
    Matrix v2(row/2);
    Matrix v3(row/2);
    Matrix v4(row/2);
    for (int i = 0; i < row; ++i) {
        for (int j = 0; j < col; ++j) {
            if(i<row/2){//上半部分
                if(j<col/2){ //左半部分
                    v1[i].push_back(a[i][j]);
                }else{ //右半部分
                    v2[i].push_back(a[i][j]);
                }
            }else{ //下半部分
                if(j<col/2){ //左半部分
                    v3[i-(row/2)].push_back(a[i][j]);
                }else{ //右半部分
                    v4[i-(row/2)].push_back(a[i][j]);
                }
            }
        }
    }
    t.push_back(v1);
    t.push_back(v2);
    t.push_back(v3);
    t.push_back(v4);
    return t;
}
//矩阵相乘
Matrix MatrixStreassen(Matrix a,Matrix b){
//    display(b);
    // 先分成四个部分
    if(a.size()==2){
        Matrix t;
        vector<int> t1,t2;
        t1.push_back(a[0][0] * b[0][0]+a[0][1] * b[1][0]);
        t1.push_back(a[0][0] * b[0][1]+a[0][1] * b[1][1]);
        t.push_back(t1);
        t2.push_back(a[1][0] * b[0][0]+a[1][1] * b[1][0]);
        t2.push_back(a[1][0] * b[0][1]+a[1][1] * b[1][1]);
        t.push_back(t2);
        return t;
    }
    // 切分成四个部分
    vector<Matrix> sa=split(a);
    vector<Matrix> sb=split(b);
    // 公式
    Matrix s1= MatrixSub(sb[1],sb[3]); // m1 的b12 -b22
    Matrix s2 = MatrixAdd(sa[0],sa[1]); //m2 的 a11+a12
    Matrix s3 = MatrixAdd(sa[2],sa[3]); // m3 的a21+a22
    Matrix s4 = MatrixSub(sb[2],sb[0]); //m4 的b21-b11
    Matrix s5 = MatrixAdd(sa[0],sa[3]); // m5 的a11+a22
    Matrix s6 = MatrixAdd(sb[0],sb[3]); //m5 的b11+ b12
    Matrix s7 = MatrixSub(sa[1],sa[3]); //m6 的 a12-a22
    Matrix s8 = MatrixAdd(sb[2],sb[3]); //m6 的 b21+b22
    Matrix s9 = MatrixSub(sa[0],sa[2]); //m7 的 a11-a21
    Matrix s10 = MatrixAdd(sb[0],sb[1]); //m7的 b11-b12
    Matrix m1 = MatrixStreassen(sa[0], s1);
    Matrix m2 = MatrixStreassen(s2, sb[3]);
    Matrix m3 = MatrixStreassen(s3, sb[0]);
    Matrix m4 = MatrixStreassen(sa[3], s4);
    Matrix m5 = MatrixStreassen(s5, s6);
    Matrix m6 = MatrixStreassen(s7, s8);
    Matrix m7 = MatrixStreassen(s9, s10);
    Matrix temp;
    temp =MatrixAdd(m5,m4);
    temp=MatrixSub(temp,m2);
    Matrix c11=MatrixAdd(temp,m6);
    Matrix c12=MatrixAdd(m1,m2);
    Matrix c21=MatrixAdd(m3,m4);
    temp=MatrixAdd(m5,m1);
    temp=MatrixSub(temp,m3);
    Matrix c22=MatrixSub(temp,m7);
    // 整合结果
    for(int i =0;i<c11.size();i++){
        c11[i].insert(c11[i].end(),c12[i].begin(),c12[i].end());
        c21[i].insert(c21[i].end(),c22[i].begin(),c22[i].end());
    }
    c11.insert(c11.end(),c21.begin(),c21.end());

    return c11;
}
// 取x的以2为底的对数 返回值为取整的，比如 1024=10 1025=10
int FastLog2(int x)
{
    float fx;
    unsigned long ix, exp;

    fx = (float)x;
    ix = *(unsigned long*)&fx;
    exp = (ix >> 23) & 0xFF;

    return exp - 127;
}
int main(){

// 用于计算的两个矩阵
// 测试例子
//    Matrix MatrixA = {
//            {1, 2, 3, 4, 5, 6, 7, 8},
//            {1, 2, 3, 4, 5, 6, 7, 8},
//            {1, 2, 3, 4, 5, 6, 7, 8},
//            {1, 2, 3, 4, 5, 6, 7, 8},
//            {1, 2, 3, 4, 5, 6, 7, 8},
//            {1, 2, 3, 4, 5, 6, 7, 8},
//            {1, 2, 3, 4, 5, 6, 7, 8},
//            {1, 2, 3, 4, 5, 6, 7, 8},
//    };
//    Matrix MatrixB = {
//            {1, 6, 7, 8, 1, 2, 3, 4},
//            {1, 6, 7, 8, 1, 2, 3, 4},
//            {1, 6, 7, 8, 1, 2, 3, 4},
//            {1, 6, 7, 8, 1, 2, 3, 4},
//            {1, 6, 7, 8, 1, 2, 3, 4},
//            {1, 6, 7, 8, 1, 2, 3, 4},
//            {1, 6, 7, 8, 1, 2, 3, 4},
//            {1, 6, 7, 8, 1, 2, 3, 4},
//    };
    long n;
    cin>>n;
    // 判断输入是否合法，符合题目规则
    if(n<0 || n % (long)pow(2,(FastLog2(2)))!=0){
        cout<<"输入非法";
        return 0;
    }
    Matrix MatrixA;
    Matrix MatrixB;
    //随机生成
    for (int i = 0; i < n; ++i) {
        vector<int> tempa;
        vector<int> tempb;
        for (int j = 0; j < n; ++j) {
            tempa.push_back((int)rand()%15+1);
            tempb.push_back((int)rand()%15+1);
        }
        MatrixA.push_back(tempa);
        MatrixB.push_back(tempb);
    }
    cout<<"________________A___________________"<<endl;
    display(MatrixA);
    cout<<"________________B___________________"<<endl;
    display(MatrixB);
    cout<<"________________结果___________________"<<endl;
    display(MatrixStreassen(MatrixA,MatrixB));
    return 0;

}

结果

总结简书

采用Strassen算法作递归运算，需要创建大量的动态二维数组，其中分配堆内存空间将占用大量计算时间，从而掩盖了Strassen算法的优势
于是对Strassen算法做出改进，设定一个界限。当n<界限时，使用普通法计算矩阵，而不继续分治递归。需要合理设置界限，不同环境（硬件配置）下界限不同
矩阵乘法一般意义上还是选择的是朴素的方法，只有当矩阵变稠密，而且矩阵的阶数很大时，才会考虑使用Strassen算法。

介绍

代码

结果

总结 简书

总结简书