树结构

树结构是一种数据结构，由节点(node)以及链接节点的边构成(edge)

基础概念

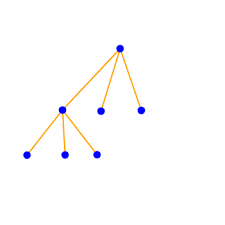
根

如果一棵树具有一个名为“根”(root)的特殊节点，那么这棵树被叫做有根树(rooted tree)

父结点子结点

有根树的节点之间具有父子关系。设一棵有根树T，他的根r到结点x的路径上的最后一条边连接结点p与结点x，此时我们将p称为x的父结点(parent)x称为p在子结点(child)

叶

我们将没有子结点的结点称为 外部结点 或者 叶节点 ，其余称为 内部结点 。

度

结点的子结点个数称为结点的度

深度

从根到x的路径长度称为x的深度，结点x到叶结点的最大路径长度称为结点x的高。根的高称为树高

二叉树

如果一棵树拥有1个根结点，且所有结点的子结点个数都不超过2,那么这棵树称为有根二叉树。

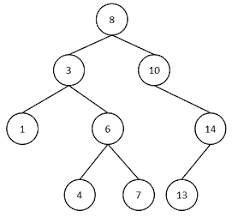
在二叉树中，每个结点的子结点数不超过2个，而且有左右结点之分。也就是说，当某个结点只存在一个子结点时，要严格区分是左结点还是右结点。我们将这各子结点有特定顺序的树称为有序树。

二叉树可以递归进行定义。二叉树条件

T没有任何结点
T由以下三个顶点集合构成
1. 根
2. 左子树
3. 右子树

有根树的表达

每个结点u的必要信息

u的结点编号

u的结点种类

u的父结点编号

u的子结点列表

u的深度

左子右兄弟表示法

信息

结点u的父结点

结点u的最左子结点

结点u的右侧紧邻兄弟结点

结构

struct Node{int parent,int left,int right};

利用u.parent可以得到各结点u的父结点。不存在父结点的为根。

不存在u.left的结点的为叶。

不存在u.right的结点的为最右侧结点

为表示根及左右结点，将NIL作为特殊结点编号。保证NIL不为一般结点使用

算法

深度

getDepth(u)
    d=0
    while T(u).parent!=NIL
    	u=T(u).parent
    	d++
    return d

深度(递归)

getDepth(u,p)
    D[u]=p
    if T[u].right!=NIL
    	getDepth(T[u].right,p)
    if T[u].left!=NIL
    	getDepth(T[u].left,p+1)

二叉树

信息

u的父结点

u的左子结点

u的右子结点

结构

struct Node{int parent,left,right};

高

setHeight(H,u)
    h1=h2=0
    if(Tu).right!=NIL
    	h1=setHeight(H,T[u].right)+1
    if(Tu).left!=NIL
    	h2=setHeight(H,T[u].left)+1
    return H[u]=max(h1,h2);

具体表达

#include<cstdio>
#define MAX 10000
#define NIL -1

struct Node{
    int parent,left,right;
};
struct Node T[MAX];
int n,D[MAX],H[MAX];

void setDepth(int u,int d){
    if(u==NIL) return;
    D[u]=d;
    setDepth(T[u].left,d+1);
    setDepth(T[u].right,d+1);
}

int setHeight(int u){
    int h1=0,h2=0;
    if(T[u].left!=NIL)
        h1=setHeight(T[u].left)+1;
    if(T[u].right!=NIL)
        h2=setHeight(T[u].right)+1;
    return H[u]=(h1>h2?h1:h2);
    
}
//返回结点u的兄弟结点
int getSibling(int u){
    if(T[u].parent==NIL) return NIL;
    if(T[T[u].parent].left!=NIL && T[T[u].parent].left !=u) 
        return T[T[u].parent].left;
    if(T[T[u].parent].right!=NIL && T[T[u].parent].right !=u) 
        return T[T[u].parent].right;
    return NIL;
   
}

void print(int u){
    printf("node %d:",u);
    printf("parent = %d,",T[u].parent);
    printf("sibling = %d,",getSibling(u));
    int deg=0;
    if(T[u].left!=NIL) deg++;
    if(T[u].right!=NIL) deg++;
    printf("degree = %d,",deg);
    printf("depth = %d",D[u]);
    printf("height = %d",H[u]);

    if(T[u].parent==NIL){
        printf(" root\n");
    }else if(T[u].left==NIL && T[u].right==NIL){
        printf(" leaf\n");
    }else{
        printf(" internal node\n");
    }
}

int main(){
    int v,l,r,root=0;
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        T[i].parent=NIL;
    }

    for(int i=0;i<n;i++){
        scanf("%d %d %d",&v,&l,&r);
        T[v].left=l;
        T[v].right=r;
        if(l!=NIL) T[l].parent=v;
        if(r!=NIL) T[r].parent=v;
    }

    for (int i = 0; i < n; i++)
    {
        if(T[i].parent==NIL) root=i;
    }
    setDepth(root,0);
    setHeight(root);
    for(int i=0;i<n;i++) print(i);
    return 0;
    
}

输入

输出结果

树的遍历

分类

前序遍历

根节点、左子树、右子树顺序访问

preParse(u)
    if u == NIL
    	return
    print u
    preParse(T[u].left)
    preParse(T[u].right)

中序遍历

左子树、根节点、右子树顺序访问

preParse(u)
    if u == NIL
    	return
    preParse(T[u].left)
    print u
    preParse(T[u].right)

后序访问

左子树、右子树、根节点顺序访问

preParse(u)
    if u == NIL
    	return
    preParse(T[u].left)
    preParse(T[u].right)
    print u

子树重建

描述

给出前序遍历和中序遍历，给出后序遍历

解答

#include<iostream>
#include<string>
#include<algorithm>
#include<vector>

using namespace std;
int n,pos;
vector<int> pre, in ,post;

void rec(int l, int r){
    if(l>=r) return;
    int root = pre[pos++];
    int m=distance(in.begin(),find(in.begin(),in.end(),root));
    rec(l,m);
    rec(m+1,r);
    post.push_back(root);
}
void solve(){
    pos=0;
    rec(0,pre.size());
    for (int  i = 0; i < n; i++)
    {
        if(i) cout<<" ";
        cout<<post[i];
    }
    cout<<endl;
    
}
int main(){
    int k;
    cin>>n;
    for(int i =0;i<n;i++){
        cin>>k;
        pre.push_back(k);
    }
    for (int i = 0; i < n; i++)
    {
        cin>>k;
        in.push_back(k);
    }
    solve();
    return 0;
}

程序设计：算法和数据结构笔记6——树形结构

树结构