归并排序

过程有些复杂，先来张动图掩饰下尴尬。

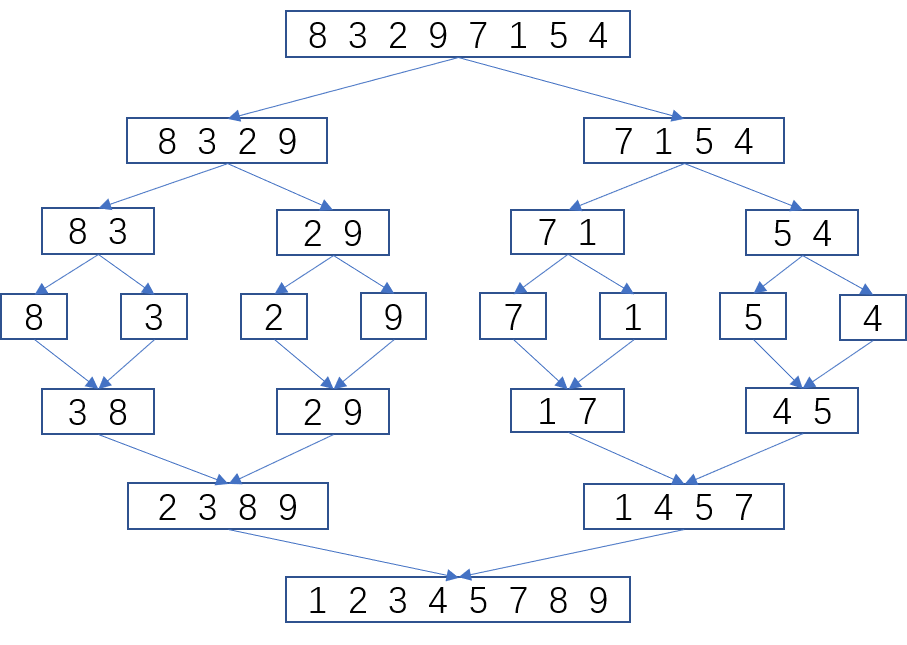
过程

将给定的包含n个元素的局部数“分割”成两个局部数组，每个数组各包含$\frac{n}{2}$个元素。（Divide）
对连个局部数组分别执行 mergeSort(归并)排序。(Solve)
通过merge将连个已经排序完成的数组“整合”成一个数组。(Conquer)

merge

对于merge过程，可以利用已经排好序的前提条件，执行$O(n1+n2)$的算法进行整合。在左半部分（L）和右半部分（R）的末尾分别安插一个 大于所有元素的标记。在比较L、R的元素过程中，只要标记设计的足够大，切将比较次数控制在$n1+n2$($right-left$)之内，就可以防止两个标记相比较。

mergeSort

mergeSort 过程中，如果局部数组只剩下一个元素时，mergeSort不做任何处理直接结束。如果不是，则计算局部数组的中央位置mid，将left到mid (不包含) 视作前半部分，mid到right(不包含)视作后半部分。递归套用mergeSort

过程实现流程

代码实现

#include<iostream>
using namespace std;
#define MAX 50000
#define SENTINEL 2000000000

int L[MAX/2+2],R[MAX/2+2];
int cnt;

void merge(int A[],int left,int mid,int right){
    int n1 = mid - left;    //左边的元素数目
    int n2 = right -mid;    //右边的元素数目
    for (int  i = 0; i < n1; i++)    L[i]=A[left+i];
    for (int  i = 0; i < n2; i++)    R[i]=A[mid+i];
    L[n1]=R[n2]=SENTINEL;   //设置最大值标志
    int i=0,j=0;
    for(int k=left;k<right;k++){
        cnt++;
        A[k]= L[i]<=R[j]? L[i++]: R[j++];
    }
}

void mergeSort(int A[],int left,int right){
    if(left+1<right){
        int mid=(left+right)/2;
        mergeSort(A,left,mid);
        mergeSort(A,mid,right);
        merge(A,left,mid,right);
    }
}
int main(){
    int A[MAX],n,i;
    cnt=0;
    cin>>n;
    for (int i = 0; i < n; i++)
    {
        cin>>A[i];
    }
    mergeSort(A,0,n);
    for (int i = 0; i < n; i++)
    {
        cout<<A[i]<<"  "; 
    }
    cout<<endl<<cnt<<endl;
    return 0;   
    
}

运行结果

一共执行34次就完成了排序

快速排序

快速排序利用基准值将数组分为两个部分，比基准值小的在基准值前面，比基准值大的在基准值后面。如果基

过程

以整个数组为对象执行quickSort
qurickSort过程:
1. 讲数组分割成前后两个局部数组
2. 对前半部分执行quickSort
3. 对后半部分执行quickSort

代码实现

#include<stdio.h>
#define Max 100000
#define SENTINEL 2000000000
int cnt;
int L[Max/2+2],R[Max/2+2];
int partition(int A[],int p,int r){
    int i,j;
    int t,x;
    x=A[r];
    i=p-1;
    for(j=p;j<r;j++){
        if(A[j]<x){
            cnt++;
            i++;
            t=A[i];
            A[i]=A[j];
            A[j]=t;
        }
    }
    t=A[i+1];
    A[i+1]=A[r];
    A[r]=t;
    return i+1;
}

void quickSort(int A[],int p,int r){
    int q;
    if(p<r){
        q=partition(A,p,r);
        quickSort(A,p,q-1);
        quickSort(A,q+1,r);
    }
}
int main(){
    int n,i,v;
    int A[Max];
    cnt=0;
    scanf("%d",&n);
    for(i=0;i<n;i++){
        scanf("%d",&A[i]);
    }
    quickSort(A,0,n-1);
    for(i=0;i<n;i++){
        printf("%d  ",A[i]);
    }
    printf("\n%d",cnt);
    return 0;
}

如果中间值选的好的话次数大大减少，在上面的同等情况下，快排仅需要20次。

利用标准库排序

sort

sort的第一个参数制定排序对象开头的迭代器，第二个参数制定末尾的迭代器(排序对象不包含末尾)，对于数组要代入指针。

STL的sort基于快排实现，并且添加了对于最坏情况的应对机制，但是 sort 属于不稳定排序算法

可以用stable_sort 基于归并排序的算法，但是耗费空间大一点，速度稍慢

sort向量代码

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main()
{
    int n;
    vector<int> v;
    cin >>n;
    for(int i=0;i<n;i++){
        int x;
        cin>>x;
        v.push_back(x);
    }
    sort(v.begin(),v.end());
    for(int i=0;i<v.size();i++){
        cout<<v[i]<<" ";
    }
    cout<<endl;
    return 0;
}

sort 数组排序

#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
    int n;
    int a[100000];
    cin >>n;
    for(int i=0;i<n;i++){
        cin>>a[i];
    }
    sort(a,a+n);
    for(int i=0;i<n;i++){
        cout<<a[i]<<" ";
    }
    cout<<endl;
    return 0;
}

https://images2018.cnblogs.com/blog/941490/201805/941490-20180514224313332-798344959.png

https://www.cnblogs.com/onepixel/p/7674659.html